Rational Contraction in Metric Space and Common Fixed Point Theorems

 Digital Object Identifier:
10.58578/ajstea.v2i1.2545
Digital Object Identifier:
10.58578/ajstea.v2i1.2545
Please do not hesitate to contact us if you would like to obtain more information about the submission process or if you have further questions.

Abstract
The study of contraction mappings in fixed-point theory is a fascinating and crucial field of mathematics. The concept of contraction plays a vital role in proving the existence and uniqueness of fixed points. Banach's contraction theory offers a fixed point theorem that is widely accepted as unique in most analyses. By using rational expressions in metric spaces, we can achieve unique results in general contraction mapping. These results are based on several innovative ideas stemming from the latest research. The delivered results upgrade and federate many existing outcomes on the topic in the literature Bhardwaj, R. et al. (2007) Chouhan et al. (2014) and Garg and Priyanka (2016). Also gives some suitable examples for verifying our results.
Citation Metrics:

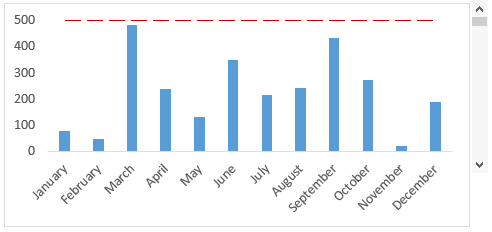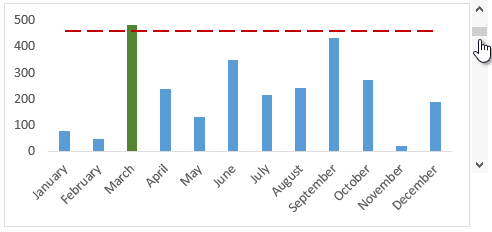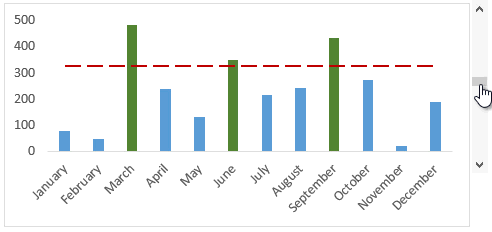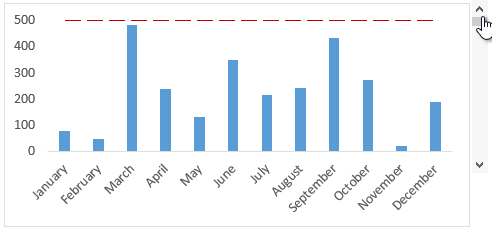
Downloads

Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
References
Banach, S. Sur les operations dans les ensembles abstraits et leur applications aux equation Integrals, Fundamental Mathematicae, 3(7), (1922), 133-181. https://doi.org/10.4064/fm-3-1131-181.
Chandok, S. , Choudhury, B.S., and Metiya, N. Fixed point results in ordered metric spaces for rational type expressions with auxiliary functions, Journal of the Egyptian Mathematical Society, 23 (2015), 95-101. http://dx.doi.org/10.1016/j.joems.2014.02.002.
Choudhury, B.S. , Metiya, N., Chakraborty, P. and Sunirmal Kundu , Multivalued mizoguchi-takahashi type rational contraction in relational metric spaces, Surveys in Mathematics and its Applications, Volume 18 (2023), 59 – 72. https://www.utgjiu.ro/math/sma.
Dass, B.K. and Gupta, S. An Extension of Banach Contraction Principle through Rational Expression, Indian J. of Pure and Applied Mathematics, 6(1975), 1455-1458.
Shakuntala Dewangan and Tiwari, S.K. Expansive Mapping in Metric Spaces and Fixed Point Theorem, International Journal of Mathematical Archive- 11(12),(2020), 1-7.
Dutta, P. N. and Choudhary, B.S. (2008), A Generalization of Contraction Principle in Metric Spaces, Fixed Point Theory and Appl., Art. Id. 406368, 8 pages. https://doi.org/10.1155/2008/406368
Khan, M. S. A fixed point theorems for metric spaces, Rendicanti Dell’I Istitute Mathematica Dell’ Universita, Trieste Int. J. Math. 8 (1976), 69-72.
Jaggi, D.S. Some unique fixed point theorems, Indian J. Pure Appl. Math, vol. 8, pp. (1977) 223-230.
Fisher, B. A fixed point theorem for compact metric spaces, Publ. Math. Debrecen 25 (1978), 193-194. https://doi.org/10.5486/pmd.1978.25.3-4.01
Jaggi, D.S. and. Dass,B.K. An extension of Banach contraction theorem through rational expression, Bull. Cal. Math.(1980), 261-266.
Bhardwaj, R., Rajput,S.S., and Yadav, R.N. Application of fixed point theory in metric spaces, Thai, J. of Mathematics, 2(2007) 253-259. www.math.science, cmu.ac.th/thaijournal
Karapinar,E., Shatanawi, W. and Tas, K. Fixed point theorem on partial metric spaces involving rational expressions, Miskolc Mathematical Notes, 14(2013),no:1, 135-142. DOI:10.18514/MMN.2013.471
. Karapinar,E., Roldan A., and Sadarangani,K. Existence and uniqueness of best proximity points under rational contractivity conditions, Mathematica Slovaca, 66,(6) (2016) 1427-1442. https://doi.org/10.1515/ms-2016-0234.
Karapinar, E., Dehici,A., and. Redjel, N. On some fixed points of α-ψ contractive mappings with rational expressions J. Nonlinear Sci. Appl., 10 (2017), 1569-1581. doi:10.22436/jnsa.010.04.23.
Fulga, A. , Fixed point theorems in rational via Suzuki approach results in nonlinear analysis,1(10 (2018) 19-29.
Fulga, A. On (ψ,ϕ)- rational contractions, Symmetry, (2020), 1-13. https://doi.org/10.3390/sym12050723.
Garg, M. (2015), A New Type Generalized Fixed Point Theorem in a Complete Metric Space, Ultra. Sci., 27(3), (2015), 1-2.
Garg, M. and Priyanka A New Generalization of Fixed Point Theorem in a Complete Metric Space, Mathematica Moravica., 28(3), (2016),179-182.
Gupta, S. and Garg, A.K., Fixed Point Theorems on Complete Metric Space, International Journal on Emerging Technologies 10(2b), (2019),109-112
Proinov, P.D., Fixed point theorems for generalized contractive mappings in metric spaces, J. fixed point theory and App. (2020) 22: 21, DOI:10.1007/s11784-020-0756-
Raji, M.and Adegboye, F. Some Fixed point theorems for rational contractions in partially ordered metric spaces, Research Square, (2022), 1-11. DOI: https://doi.org/10.21203/rs.3.rs-1818692/v1
Rao, N. S. and Kalyani, K. (2021), Generalized fixed point results of rational type Contractions in partially ordered metric spaces, BMC Res Notes 14:390, (2021), 1-13. https://doi.org/10.1186/s13104-021-05801-7.
Rao.N.S. , Kalyani, K. and Gemechu,T. Fixed Point Theorems in Partially Ordered Metric Spaces with Rational Expressions, Information Sciences Letters,10(3),(2021), 451-460. doi:10.18576/isl/100309
Shirivastava, R., Dubey, K.R. and Tiwari, P. Common Fixed Point Theorems in Complete Metric Space, Advances in applied sciences research, 4(6), (2013), 82-89.www.pelagaesearchlibrary.com
Shrivastava, R., Sharma, M. and Bhardwaj, R.,Fixed point theorems in complete metric space. Journal of multidisciplinary Engineering Science and Technology, 1(4), (2014), 21-27.